Generative AI (aka GenAI) is reworking the world with a plethora of functions together with chatbots, code era, and synthesis of photographs and movies. What began with ChatGPT quickly led to many extra merchandise like Sora, Gemini, and Meta-AI. All these fabulous functions of GenAI are constructed utilizing very giant transformer-based fashions which are run on giant GPU servers. However as the main focus now shifts in the direction of customized privacy-focused Gen-AI (e.g., Apple Intelligence), researchers are attempting to construct extra environment friendly transformers for cell and edge deployment.
Transformer-based fashions have develop into state-of-the-art in nearly all functions of pure language processing (NLP), laptop imaginative and prescient, audio processing, and speech synthesis. The important thing to the transformer’s capability to be taught long-range dependencies and develop a worldwide understanding is the multi-head self-attention block. Nevertheless, this block additionally seems to be essentially the most computationally costly one, because it has quadratic complexity in each time and area. Thus, with the intention to construct extra environment friendly transformers, researchers are primarily specializing in:
- Creating linear complexity consideration blocks utilizing the kernel trick
- Lowering the variety of tokens that participate in consideration
- Designing alternate mechanisms for consideration
On this article, we will undergo these approaches to supply an outline of the progress in the direction of environment friendly transformer growth.
Multi-Head Self Consideration (MHSA)
In an effort to talk about environment friendly transformer design, now we have to first perceive the Multi-Head Self Consideration (MHSA) block launched by Vaswani et al. of their groundbreaking paper “Consideration Is All You Want.” In MHSA, there are a number of similar self-attention heads and their outputs are concatenated on the finish. As illustrated within the determine under, every self-attention head tasks the enter x into three matrices — queries Q, keys Ok, and values V of sizes — N x d the place N is the variety of tokens and d denotes the mannequin dimension. Then, the eye, A computes the similarity between queries and keys and makes use of that to weigh the worth vectors.
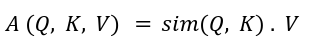
In MHSA, scaled-softmax is used because the similarity kernel:
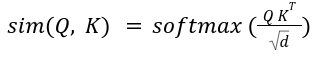
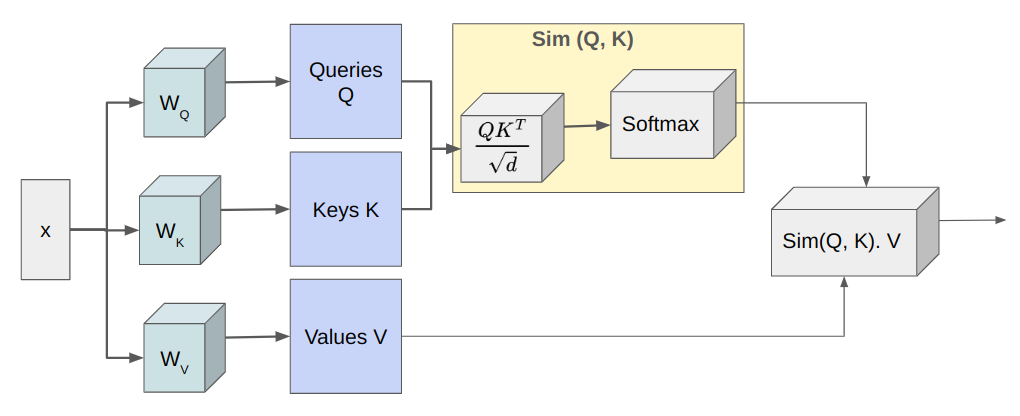
Computing the dot product of Q and Ok is of complexity O (N^2 d), so the latency of MHSA scales poorly with N. For photographs, N = HW the place H and W are the peak and width of the picture. Thus, for higher-resolution photographs, latency will increase considerably. This quadratic complexity is the largest problem within the deployment of those vanilla transformer fashions on edge units. The subsequent three sections elaborate on the strategies being developed to cut back the computational complexity of self-attention with out sacrificing efficiency.
Linear Consideration With Kernel Trick
Softmax consideration will not be fitted to linearization. Therefore, a number of papers have tried to discover a appropriate decomposable similarity kernel that may permit altering the order of matrix multiplication to cut back latency. As an instance, for some function illustration operate F(x), such that:
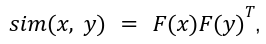
We will get hold of similarity kernel as:
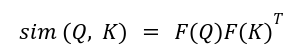
In order that the eye could be written as:
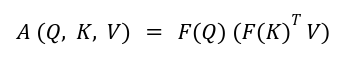
By first multiplying Key and Worth matrices, we scale back the complexity to be O (N d^2), and if N , then the complexity of consideration operation is diminished from quadratic to linear.
The next papers select completely different function illustration features F(x) to approximate the softmax consideration and attempt to obtain comparable or higher efficiency than the vanilla transformer however for a fraction of time and reminiscence prices.
1. Elu Consideration
The “Transformers are RNNs” paper chosen the next function illustration operate to acquire a constructive similarity matrix:
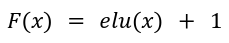
The place elu(x) is exponential linear unit with a > 0 outlined as:
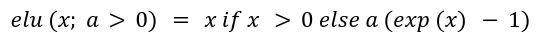
They selected elu(x) over ReLU(x) as they didn’t need the gradients to be zero when x .
2. Cosine Similarity Consideration
The cosFormer paper acknowledged that softmax dot-product consideration has the capability to be taught long-range dependencies. The authors attributed this capability to 2 essential properties of the eye matrix: first, the eye matrix is non-negative, and second, the eye matrix is concentrated by a non-linear re-weighting scheme. These properties fashioned the premise of their linear alternative for the softmax consideration.
In an effort to preserve the non-negativity of the eye matrix, the authors used ReLU as a metamorphosis operate and utilized it to each question Q and key Ok matrices. After that, cosine re-weighing was performed as cos places extra weights on neighboring tokens and therefore, enforces locality.
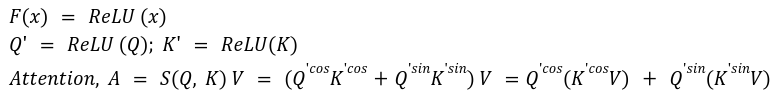
3. Hydra Consideration
The Hydra Consideration paper additionally used the kernel trick to first change the order of multiplication of matrices. The authors prolonged the multi-head idea to its excessive and created as many heads because the mannequin dimension d. This allowed them to cut back the eye complexity to O (Nd).
Hydra consideration entails an element-wise product between Key and Worth matrices after which sums up the product matrix to create a worldwide function vector. It then makes use of the Question matrix to extract the related data from the worldwide function vector for every token as proven under.
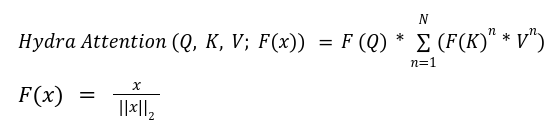
The place * represents the element-wise product and the operate F(x) in Hydra consideration is L2-Normalization in order that the eye matrix is principally cosine similarity. The summation represents combining data from all heads.
4. SimA Consideration
The SimA paper recognized that within the common consideration block, if a channel within the Q or Ok matrix has giant values, then that channel can dominate the dot product. This subject is considerably mitigated by multi-head consideration. In an effort to preserve all channels comparable, the authors selected to normalize every channel of Q and Ok by the L1-Normalization alongside the channel dimension. Thus, L1-Normalization is used because the function illustration operate to switch the softmax operate.
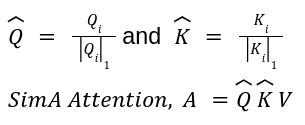
The place the order of multiplication relies on if N > d or N
Additional, not like vanilla transformer architectures, the interactions between question and key are allowed to be destructive. This signifies that one token can probably negatively have an effect on one other token.
Lowering the Variety of Tokens
This class of papers focuses on decreasing the variety of tokens, N, that participate within the consideration module. This helps to cut back the variety of computations whereas nonetheless sustaining the identical mannequin efficiency. Because the computational complexity of multi-head self-attention is quadratic in N; therefore, this strategy is ready to carry some effectivity into transformer fashions.
1. Swin Transformer
Swin Transformer is a hierarchical transformer structure that makes use of shifted-window consideration. The hierarchical construction is much like convolutional fashions and introduces multi-scale options into transformer fashions. The eye is computed in non-overlapping native home windows that are partitions of a picture. The variety of picture patches in a window partition is fastened, making the eye’s complexity linear with respect to the picture dimension.
The eye mechanism of the Swin Transformer consists of Window-Multihead Self Consideration (W-MSA) adopted by Shifted Window-Multihead Self Consideration module (SW-MSA). Every of those consideration modules applies self-attention in a set window partition of dimension M x M which is impartial of picture decision. Solely within the case of SW-MSA, home windows are shifted by M/2, which permits for cross-window connections and will increase the modeling energy. Since M is fixed, the computational complexity turns into linear within the variety of picture patches (tokens). Thus, the Swin transformer builds a extra environment friendly transformer by sacrificing world consideration but it surely limits the mannequin’s capability to have a really long-range understanding.
2. ToSA: Token Selective Consideration
The ToSA paper launched a brand new Token-Selector module that makes use of consideration maps of the present layer to pick out “important” tokens that ought to take part within the consideration of the following layer. The remaining tokens are allowed to bypass the following layer and are merely concatenated with the attended tokens to kind the entire set of tokens. This Token-Selector could be launched in alternate transformer layers and may also help scale back the general computations. Nevertheless, this mannequin’s coaching mechanism is kind of convoluted involving a number of phases of coaching.
Alternate Consideration Mechanisms
This class of papers makes an attempt to switch the multi-head self-attention with extra scalable and environment friendly consideration mechanisms. They often make use of convolutions and reordering of operations to cut back computational complexity. A few of these approaches are described under.
1. Multi-Scale Linear Consideration
The EfficientViT paper additionally used the kernel trick to cut back the computational complexity of the transformer block to linear within the variety of tokens. The authors chosen ReLU because the function transformer operate F(x). Nevertheless, they observed that ReLU creates fairly subtle consideration maps in comparison with Softmax Scaled Dot-Product consideration. Therefore, they launched small-kernel depth-wise convolutions utilized individually to Question Q, Key Ok, and Worth V matrices adopted by ReLU Consideration to raised seize the native data. In whole, this consideration block entails three ReLU attentions one every on – Q, Ok, and V, 3×3 DepthWise-Conv of Q, Ok, V and 5×5 DepthWise-Conv of Q, Ok, V. Lastly, the three outputs are concatenated.
2. Transposed Consideration
The EdgeNeXt paper preserved the transformer’s capability to mannequin world interactions by maintaining the dot-product consideration. Nevertheless, the paper used a transposed model of consideration, whereby the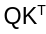 
is changed by:
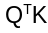This modifications the dot-product computation from being utilized throughout spatial dimensions to being utilized throughout channel dimensions. This matrix is then multiplied with values V after which summed up. By transposing the dot product, the authors scale back the computation complexity to be linear within the variety of tokens.
3. Convolutional Modulation
The Conv2Former paper simplified the eye mechanism by utilizing a big kernel depth-wise convolution to generate the eye matrix. Then, element-wise multiplication is utilized between the eye and worth matrices. Since there is no such thing as a dot product, computational complexity is diminished to linear. Nevertheless, not like MHSA, whose consideration matrix can adapt to inputs, convolutional kernels are static and lack this capability.
4. Environment friendly Additive Consideration
The SwiftFormer paper tried to create a computationally cheap consideration matrix that may be taught world interactions and correlations in an enter sequence. That is achieved by first projecting the enter matrix x into question Q and key Ok matrices. Then, a learnable parameter vector is used to be taught the eye weights to provide a worldwide consideration question q. Lastly, an element-wise product between q and Ok captures the worldwide context. A linear transformation T is utilized to the worldwide context and added to the normalized question matrix to get the output of the eye operation. Once more, as solely element-wise operations are concerned, the computational complexity of consideration is linear.
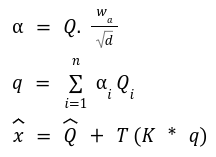
The Street Forward
Creating environment friendly transformers is important for getting the very best efficiency on edge methods. As we transfer in the direction of extra customized AI functions working on cell units, that is solely going to achieve extra momentum. Though appreciable analysis has been performed, nonetheless, a universally relevant environment friendly transformer consideration with comparable or higher efficiency than Multi-Head Self Consideration continues to be an open problem. Nevertheless, for now, engineers can nonetheless profit from deploying a number of of the approaches coated on this article to steadiness efficiency and effectivity for his or her AI functions.