“Start With Why”
Queues are a built-in mechanism in all places in at present’s software program. Not being conversant in the fundamentals of queuing idea will stop you from understanding the relations between latency and throughput, high-level capability estimations, and workload optimization. Understanding the internals of queuing fashions is definitely not that arduous to understand. On this article, I am going to sum up the essence of what is required for a software program engineer to be simpler of their subject.
Queues Are In all places!
Let’s examine some frequent examples from a mean dude’s vocabulary (like me). I am going to listing among the know-how usages of queues with out even interested by it.
- Java’s fork-join swimming pools use a number of queues with a work-stealing mechanism.
- In distinction, all of the old-school Java thread swimming pools use unbounded queues by default — inflicting latency and reminiscence issues.
- Resilience4J has many implementations involving queuing, like bulkheads.
- All of the generally recognized pub-sub brokers contain the utilization of queues — together with Kafka, RabbitMQ, and so forth. Redis affords pubsub mechanism as nicely.
- In fact, a mean working system has a number of built-in work queues, together with CPU run queue, disk IO queue, community interfaces have ring buffers, and so forth.
The Fundamentals
Let’s cowl the essential ideas first earlier than we focus on sensible functions. What are the important thing metrics which might be in play, after we’re investigating a queue? We’ve got the next related metrics when speaking about queues usually.
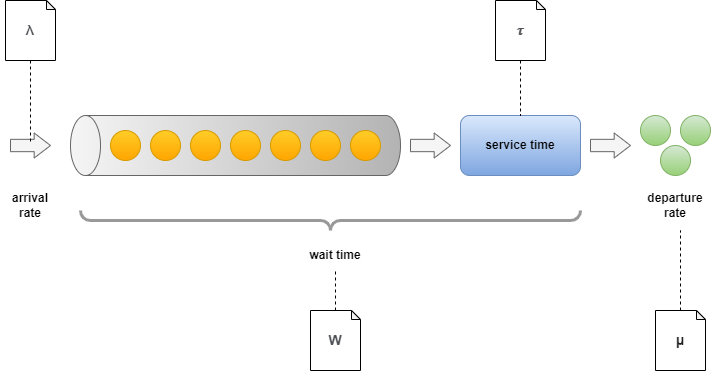
Description of Every Time period
- Arrival charge: (lambda) — The speed at which new work objects arrive within the queue.
- Wait time: (W) — The entire time spent by every work merchandise within the system. Normally composed of two components. Time spent within the queue (decided by previous work objects) and time spent with service.
- Servers: (c) — Referring to the extent of parallelization.
- Service time: (tau=1/mu) — The time required to course of a single work merchandise. It is typically translated to charge and known as departure charge.
- Departure charge: (mu) — The speed at which objects are processed.
- Utilization: (rho=lambda/mu) — Merely describes the ratio between arrival and departure charge.
- Variety of objects being served (L): Complete components within the system, together with these being processed and ready within the queue.
Matching With Sensible Naming and Notation
In software program engineering, we use barely completely different phrases when speaking about efficiency. You’ll find a mapping between the notation utilized in queuing idea and their counterpart:
| Naming in mannequin | Naming in software program methods | Description |
|---|---|---|
| arrival charge/departure charge | throughput/load | It is good to differentiate between the 2 relying on the context. Arrival charge sometimes called load, load common |
| wait time | latency | None of them distinguishes between wait time within the queue and ready due to being served. |
| servers | executors/processors | We largely imply the variety of CPUs/staff on that |
| service time | execution time/length | Measured because the time required to do a single process. Typically simply blended with latency. |
| utilization | utilization | Virtually utilization is calculated with varied strategies. Typically it means the ratio of unutilized CPU ticks and utilized ones over a given time window (e.g. 5 seconds). |
| queue size | saturation | Most frequently they point out the identical factor: What’s the additional workload the system has to deal with? The most well-liked utilization of the time period “saturation” comes from the 4 golden alerts talked about within the Google SRE ebook. |
Easy Use-Circumstances
Sequential
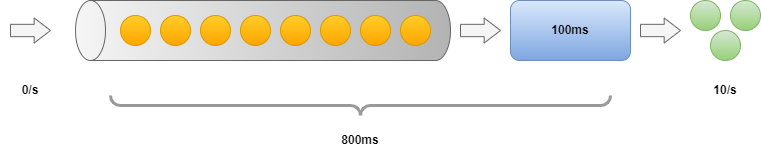
Now we could say having a easy queue just like the one above. We’ve got 8 objects within the queue and no new arrivals, The execution length is 100 ms. What are the throughput and latency? We are able to produce a inexperienced marble in each 100 ms, so that provides us 10 /s. The latency is a bit trickier to find out. The primary merchandise may have 100 ms latency. The final merchandise requires all of the earlier ones to be processed, so its latency shall be 8 * 100ms. So the minimal latency is 100 ms, the utmost is 800 ms and the imply is 450 ms.
Parallel
Let’s attempt to enhance the variety of executors. How the earlier use-case is altering if we add one other one?
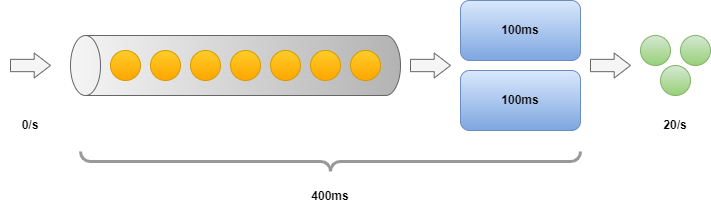
We are able to now produce 2 work objects in each 100 ms, so throughput is doubled to 20/s. The primary merchandise requires 100 ms to course of and the final one wants 400 ms (we will take 2 objects on every 100 ms interval). So the minimal latency is 100 ms, the utmost is 400 ms and the imply is 250 ms.
A right away vital commentary to make is that the latency we’re experiencing is set by the place we’re sitting within the queue: If the queue is empty or almost empty — scaling out has actually no impact on the latency. As we’ll see within the upcoming sections, having an elevated quantity of labor objects queued up has its personal unfavourable implications.
Pipelines
How do issues change if we break up the work in another way than within the earlier instance? Let’s assume we now have two queues connected to one another with two executors. The general execution time would be the similar as earlier than. Will splitting the work have any impact on the latency/throughput?

We are able to now produce 1 work merchandise in each 50 ms doubling our throughput to 20 /s. The primary merchandise nonetheless requires 100 ms to go by means of, however the final one solely wants 450 ms. Think about that after the primary 100 ms – when the primary merchandise is processed we will see a brand new inexperienced marble in every 50 ms till the queue will get empty. The minimal latency is 100 ms, the utmost is 450 ms and the imply is 275 ms.
That is the place the facility of reactive libraries comes from. Regardless that you may assume you write a sequential code it isn’t executed as-is. Solely your declaration of causation is sequential. You are declaring a pipeline of execution that splits your general workload into smaller items and runs it in parallel. I can point out loads of examples, like Kotlin coroutines, Java completable futures, the ReactiveX library, Akka, and so forth. The commentary above remains to be true: Latency just isn’t altering if our queues have only some components
As you possibly can see from the latency numbers above — minimal values do not expose an excessive amount of concerning the queue size. Alternatively, most latencies can point out saturation: it tells you the way a lot time is spent on the queue all through the system. If you do not know a lot concerning the length of execution a option to get a touch on the saturation of a black-box system is to regulate max(latency) — min(latency) or p99(latency) — avg(latency)
One other good way of visualizing latency distributions and getting hints on saturations is by utilizing heatmaps.
Bottleneck
What occurs in these circumstances, when we’ve got one executor within the pipeline whose latency takes nearly all of the time? Let’s examine the instance under:

You possibly can take into consideration this case as quite a lot of the primary train: Throughput is set by the slowest executor because it’s “choking” our pipeline. So we will solely produce a marble in every 100 ms giving us the general 10/s. The latency most is identical as for the primary train, besides that we’ve got to pay a further penalty of +50 ms for every operation. So now we’ve got a minimal latency of 150 ms, a imply of 500 ms, and a most of 850 ms.
When we’ve got a bottleneck in a scenario as above, specializing in the slowest execution brings essentially the most profit. Be at liberty to match the numbers with the earlier train. We’re benefiting from speedup each in latency and throughput.
Superior Use-Circumstances
To have the ability to examine extra superior use circumstances, we’re shifting gears. I will use this straightforward modeling library for the following couple of sections.
Secure and Unstable Conditions
What occurs if the utilization is increased than 100%? In these circumstances, the arrival charge is bigger than our general throughput. How is it affecting our latency? Our arrival interval (100ms) goes to be a bit lower than our execution interval (120ms).
import matplotlib.pyplot as plt
import numpy as np
from src.queue import Queue
%matplotlib inline
plt.rcParams["figure.figsize"] = (12, 6) # (w, h)
SAMPLE_SIZE = 100
ARRIVAL_INTERVAL = 100
EXECUTION_INTERVAL = 120
EXECUTORS = 1
inter_arrival_time = np.full(form=SAMPLE_SIZE, dtype=int, fill_value=ARRIVAL_INTERVAL)
queue = Queue(inter_arrival_time, np.full(form=SAMPLE_SIZE, dtype=int, fill_value=EXECUTION_INTERVAL), executors=EXECUTORS)
queue.course of()
fig, (queue_length, latency) = plt.subplots(1, 2)
queue_length.set_title("Queue length")
queue_length.set(xlabel=r'Time ($ms$)', ylabel=r'Size ($L$)')
queue_length.plot(*zip(*queue.length_with_timestamps), alpha=0.5)
latency.set_title("Latency")
latency.set(xlabel="Index", ylabel=r'Period ($ms$)')
latency.plot(queue.wait_times, alpha=0.5)
fig.tight_layout()
plt.present()
print(f'Latency min: {queue.wait_times.min()}')
print(f'Latency common: {queue.wait_times.imply()}')
print(f'Latency max: {queue.wait_times.max()}')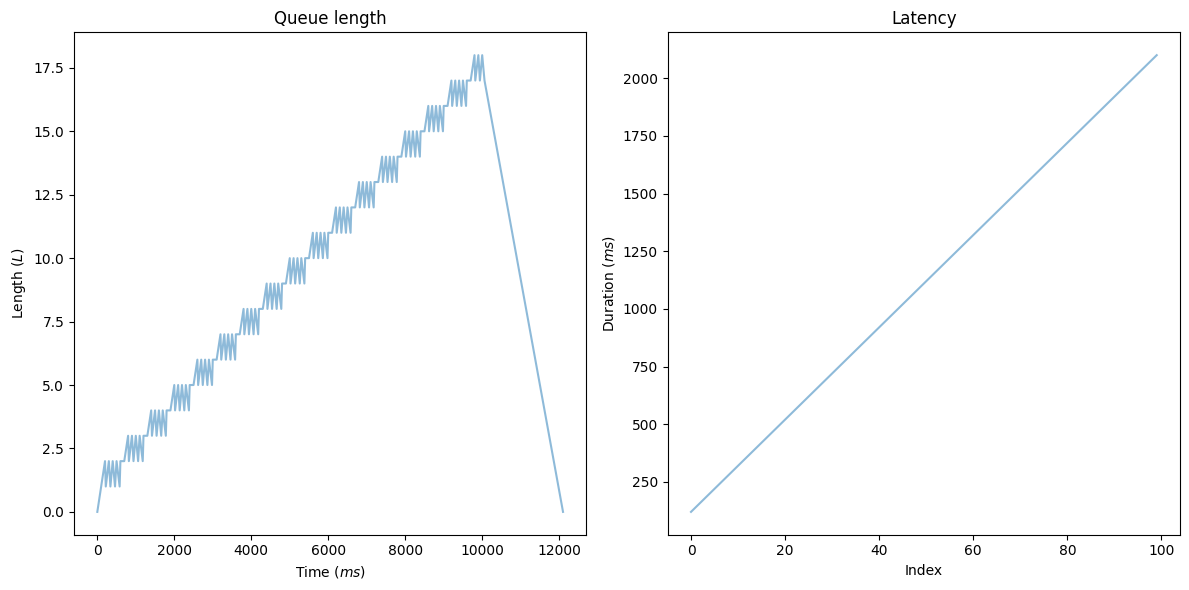
The queue size exhibits a linearly rising variety of components. After we attain the SAMPLE_SIZE, the arrival charge drops to zero and the queue dimension begins reducing linearly. The time window equals the entire time required to course of all the things: execution time * SAMPLE_SIZE. What does the diagram on the fitting inform us? We’ve got a constantly rising latency.
If the arrival charge is bigger than your throughput, your system should take motion. You’ve two choices right here:
- Scaling out executors: Bear in mind what I stated earlier about decreasing latency by scaling out? Growing the variety of executors will enhance latency till the utilization reaches 100% (e.g. you stabilize). Scaling out just isn’t a possible choice to enhance latency over that time.
- Utilizing charge limiting and rejecting new arrivals: Successfully this may be finished by limiting the queue dimension.
Scaling Out
Let’s examine what occurs after we scale out the variety of executors on this case:
from ipywidgets import interactive
from src.queue import timestamps_to_intervals
def display_queue_metrics(executrs):
inter_arrival_time = np.full(form=SAMPLE_SIZE, dtype=int, fill_value=ARRIVAL_INTERVAL)
fig, (queue_length, wait_times) = plt.subplots(1, 2)
queue = Queue(inter_arrival_time, np.full(form=SAMPLE_SIZE, dtype=int, fill_value=EXECUTION_INTERVAL), executors=executrs)
queue.course of()
wait_times.set_title("Latency")
wait_times.set(xlabel="Time", ylabel=r'Period ($ms$)')
wait_times.plot(queue.wait_times, alpha=0.5)
queue_length.set_title("Queue length")
queue_length.set(xlabel="Time", ylabel=r'Size ($L$)')
queue_length.plot(*zip(*queue.length_with_timestamps), alpha=0.5)
fig.tight_layout()
plt.present()
interactive_plot = interactive(
display_queue_metrics,
executrs=(1, 8)
)
interactive_plot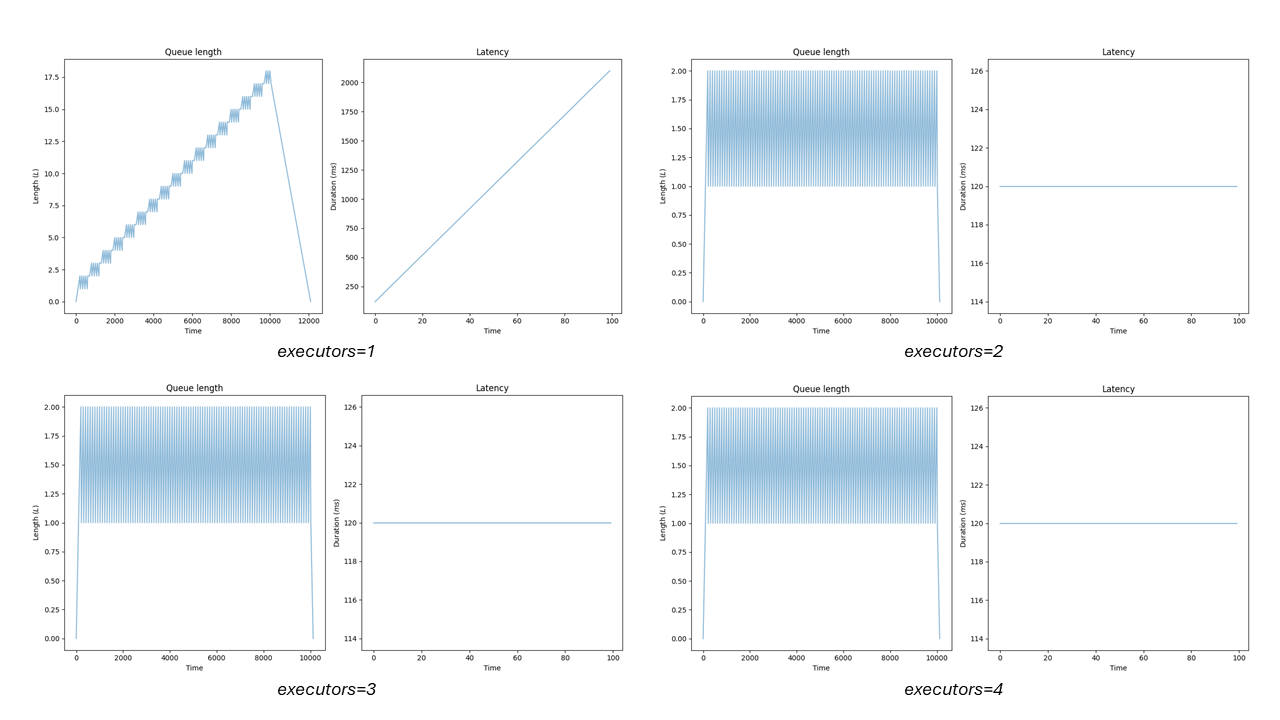
After you scale out to a degree, the place utilization is secure the saturation is eradicated. Latency is sure to the execution length and also you get no additional achieve from including extra executors. In these circumstances, latency ought to fluctuate a bit however it’s primarily decided by the execution length. That is the rationale why p99(latency) — avg(latency) is an effective indicator of saturation if a metric of queue dimension just isn’t out there.
Capability Planning: From DAU to Throughput
How can we use queuing fashions to foretell workloads? The complexity of this process arises from the unknown issue of the arrival distribution: How ought to I mannequin the consumer conduct? As a result of the general utilization of our system just isn’t fixed. There’s often a peak interval sure to weekends or out-of-office hours. If we observe the requests coming in, they typically kind a wavelike sample, and peak masses can double the typical. Even worse — the steepness is often completely different on all sides. Right here comes Little’s legislation into play.
OK, now we could say we’ve got 100,000 DAU. How can we convert this to any significant throughput? Assuming the considering time of z and common latency r, every request requires the entire latency of z+r. Normally, on the edge, r will be derived from customary internet efficiency metrics. It ought to be lower than 2 seconds as a common rule of thumb. Estimated considering time is roughly double for that quantity, so 4 sec is an effective “guestimate”, giving us minimal latency of z+r = 6 sec. If every “user” is evenly distributed over 24 hours, that would supply us L = 70 customers in every minute-long window. Throughput ought to match our arrival charge, so we’d like Little’s legislation to grasp how one can calculate the arrival charge from the given numbers.
Little’s Regulation
Little’s legislation merely states: L = lambda * W. Utilizing the phrases under, this may imply within the case above that lambda = L / W or lambda = 70/(6*60) in our case. So we should always anticipate ~0.2 ops/min on common from this technique.
Be aware: All the time confirm and re-evaluate your estimations with actual numbers to have an general impression of your mannequin’s accuracy.
Wavelike Patterns
It is vital to make clear that Little’s legislation mentions averages. It additionally states that the distribution and scheduling usually are not affecting these numbers general. It is also unbiased from the extent of parallelization, or ordering of sub-tasks. So it doesn’t rely what number of cases you have got, or what number of distant calls are in your crucial path. Easy as that. For extra on this, I invite you to discover this Jupyter pocket book.
Let’s examine the above in follow: What if we’ve got to provision for peak load? Let’s generate a wavelike sample and examine how our queuing mannequin behaves:
NUMBER_OF_SAMPLES = 100
BASELINE_ARRIVAL_RATE = 50
PEAK_ARRIVAL_RATE_RATIO = 2.5
STEEPNESS = 6.
# A easy wave sample generator (primarily based on instance https://numpy.org/doc/secure/reference/random/generated/numpy.random.weibull.html)
def weibull_distr(x,n,a):
return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)
arrival_rate = np.array([
(weibull_distr(x/NUMBER_OF_SAMPLES*2, 1., STEEPNESS) / PEAK_ARRIVAL_RATE_RATIO + 1) * BASELINE_ARRIVAL_RATE
for x in range(1,NUMBER_OF_SAMPLES)
])
plt.title("Arrival rate over time")
plt.ylabel("Rate ($ops/s$)")
plt.xlabel("Index")
plt.plot(arrival_rate, alpha=0.5, label="rate")
plt.axhline(y=arrival_rate.imply(), colour="y", linestyle="-.", label=f'common ({arrival_rate.imply():.2f})')
plt.axhline(y=arrival_rate.max(), colour="grey", linestyle="-.", label=f'peak ({arrival_rate.max():.2f})')
plt.legend()
plt.present()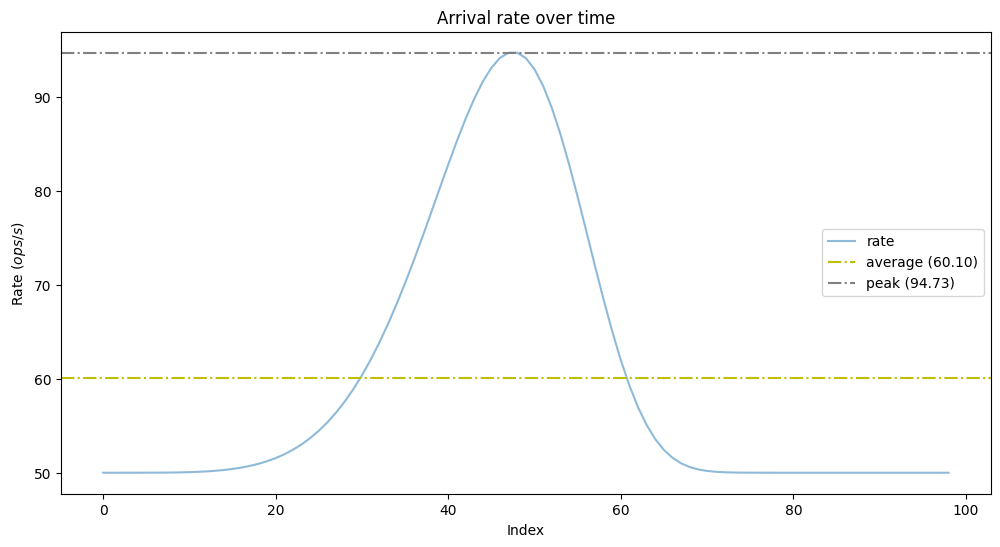
As we will see we’ve got the baseline arrival charge of 50 ops/s, the utmost doubled at 95 ops/s, and the imply is 60 ops/s. Is it sufficient to comply with Little’s legislation blindly and provision to common throughput on this case? What would be the latency on the peak in the course of the utilization enhance? Let’s mannequin this instance to reply these questions.
# Have a bit sooner throughput, than arrival charge.
THROUGHPUT_MULTIPLIER = 1.2
service_rate = arrival_rate.imply() * THROUGHPUT_MULTIPLIER
service_intervals = np.full(form=len(arrival_rate), dtype=float, fill_value=1 / service_rate)
queue = Queue(1 / arrival_rate, service_intervals, executors=1)
queue.course of()
fig, (queue_length_time, wait_times) = plt.subplots(1, 2)
queue_length_time.set_title("Queue length")
queue_length_time.set(xlabel="Time", ylabel=r'Size ($L$)')
queue_length_time.axhline(y=queue.size.imply(), colour="y", linestyle="-.", label=f'common ({queue.size.imply():.2f})')
queue_length_time.plot(*zip(*queue.length_with_timestamps), alpha=0.5, label="length")
queue_length_time.legend()
wait_times.set_title("Latency")
wait_times.set(xlabel="Index", ylabel=r'Period ($s$)')
wait_times.axhline(y=queue.wait_times.imply(), colour="y", linestyle="-.", label=f'common ({queue.wait_times.imply():.2f})')
wait_times.plot(queue.wait_times, alpha=0.5, label="latency")
wait_times.legend()
fig.tight_layout()
plt.present()We’ve got 120% of the imply arrival charge for this era. It will permit us to course of all the weather in the course of the peak interval with a most latency of 60 ms. Altering the ratio between throughput and imply arrival charge will end in a unique most latency for peak durations. Total the skilled latency throughout peaks was decided roughly by these components:
- The ratio of most and imply arrival charge (right here we had roughly double of the baseline).
- The ratio between throughput and imply arrival charge (how a lot we overprovision).
Why does this matter and why cannot we simply depend on autoscaling? It primarily is determined by our scaling efficiency. Typically bootstrapping and warming up new cases requires even 30 sec! Throughout this era the remainder of the cases should deal with extra load than common. With the mannequin above we will higher estimate their conduct and the anticipated latency penalty. Additionally vital — your queues present backpressure, allowing the underlying infrastructure to outlive throughout brief bursts of visitors.
Artificial Workloads
The arrival distribution will be varied — think about a scenario the place you have got evenly distributed IoT visitors over the entire day. By writing an experiment just like the one above you can also make your personal analysis. No have to do an elaborate efficiency take a look at to get some tough numbers. Comparable questions might come up from varied situations when a dependable queuing mannequin can help us. Typical use circumstances we have to examine could possibly be:
- Can we scale back latency by doubling the variety of cases for a given situation? What is the anticipated latency?
- Can we hold our SLA by having a ninetieth percentile latency of 100 ms with 120% of the present load?
- What number of staff do I would like for a given charge of requests over a pub-sub matter if the latency cannot exceed 500 ms?
Monitoring Queues: Autoscaling
In abstract, as I discussed earlier than queues are both full or almost empty. The entire above hints that we should actively monitor queue size and utilization. It appears to be a good suggestion to attach these two metrics with autoscaling: Scaling out improves latency after we’re overutilized and the profit on latency turns into zero after a sure level. However what is the supreme goal utilization? To grasp this worth higher, we’d like motive concerning the variance of the incoming load. It is not often evenly distributed. For this particular situation, we’ll assume that there could possibly be outliers and use an exponential distribution for the arrival charge. We’ll have a hard and fast execution charge of 50 ops/s and an rising imply arrival charge from 1 ops/s to 50 ops/s
EXECUTION_RATE = 50
SAMPLE_SIZE = 5000
mean_arrival_rates = np.array(vary(1, 50))
# arrival charge -> ms
def get_mean_wait_times(mean_arrival_rate):
execution_interval_in_ms = 1/EXECUTION_RATE * 1000
mean_arrival_interval_in_ms = 1/mean_arrival_rate * 1000
queue = Queue(
np.random.exponential(scale=mean_arrival_interval_in_ms, dimension=SAMPLE_SIZE),
np.full(form=SAMPLE_SIZE, dtype=float, fill_value=execution_interval_in_ms)
)
queue.course of()
return queue.wait_times.imply()
plt.title("Latency over Utilization")
plt.xlabel(r'Utilization ($%$)')
plt.ylabel(r'Latency ($ms$)')
plt.plot(
mean_arrival_rates / EXECUTION_RATE * 100,
[ get_mean_wait_times(rate) for rate in mean_arrival_rates ],
alpha=0.5
)
plt.present()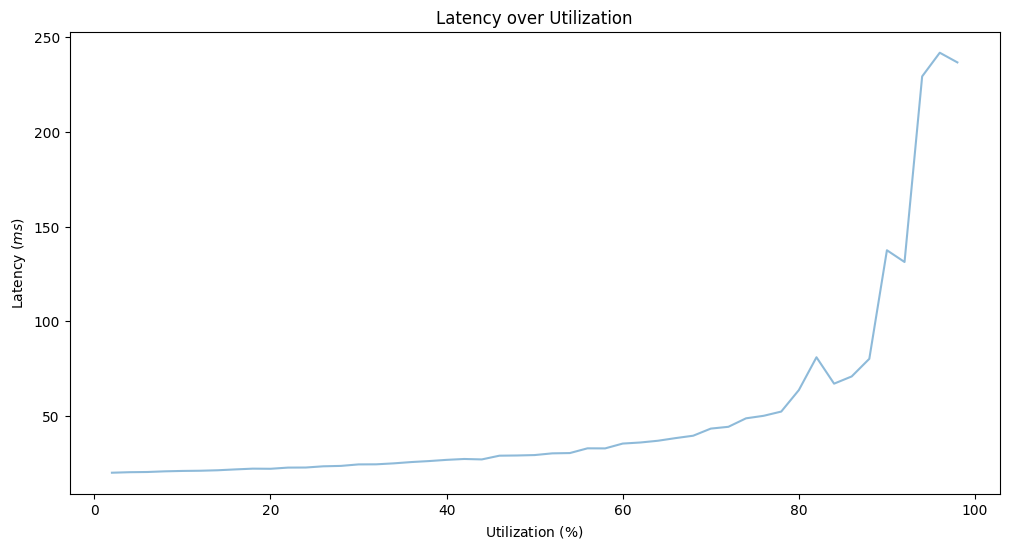
Primarily based on the mannequin if we need to hold the latency below 50 ms, we won’t have utilization bigger than 60%. Be aware, that this mannequin is contemplating the variance of the arrival charge, by not utilizing a relentless charge. For extra about this matter, be happy to research M/D/1 queues and associated formulation. The impact of variance on the latency for top utilization is additional expressed by Kingman’s formulation. Larger variance requires decrease utilization to fulfill our latency goal.
Monitoring Targets
To grasp our system higher, good targets for monitoring could possibly be:
- Queue size (if the chosen know-how permits it)
- The distinction between p99 and imply latency can trace on the queue size, as we have seen within the first fundamental examples and calculations.
- Latency distribution and warmth maps — See Brendan Gregg’s detailed article.
- Latency on every layer and the distinction between them
Further Examples
Should you nonetheless have not misplaced your urge for food for queue fashions, I encourage you to discover additional examples beginning with those under:

